сли в электростатическом поле точечного заряда  из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд  (рис. 1.8), то кулоновская сила , приложенная к заряду, совершает работу. Работа, совершаемая силой  на элементарном перемещении  равна:
    

       Так как  то
     Работа при перемещении заряда  из точки 1 в точку 2 определяется выражением:
    

    (1.10)

     т.е. не зависит от траектории перемещения заряда, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а кулоновские силы – консервативными силами.
    

     Из формулы (1.10) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.
    

     (1.11)

     Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на перемещении  будет равна  где  проекция вектора  на направление элементарного перемещения. Тогда формулу (1.11) можно записать в виде  
    

    (1.12)

      Этот интеграл называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (1.12), является потенциальным. Из обращения в нуль циркуляции вектора  следует, что линии напряженности электростатического поля не могут быть замкнутыми: они начинаются и оканчиваются на зарядах (положительных и отрицательных) или же уходят в бесконечность.
     Формула (1.12) справедлива только для электростатического поля; для электрического поля движущихся зарядов циркуляция вектора напряженности отлична от нуля.
     Тело, находящееся в потенциальном поле сил, в частности, в электростатическом поле, обладает потенциальной энергией, за счет которой силами поля совершается работа. Поэтому работу кулоновских сил (формула (1.10)) можно представить как разность потенциальных энергий, которыми обладает точечный заряд  в начальной и конечной точках поля заряда :  
    

      (1.13)

     Таким образом, потенциальная энергия заряда  в поле заряда  равна
    

     где С – постоянная интегрирования, которая определяется из граничных условий. При  потенциальная энергия  и . Следовательно, потенциальная энергия заряда , находящегося в поле заряда  на расстоянии r от него, равна:
    

           (1.14)

     Если поле создается системой из n точечных зарядов  то работа электростатических сил, совершаемая над зарядом , равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия  заряда , находящегося в этом поле, равна сумме его потенциальных энергий в полях, создаваемых каждым из зарядов в отдельности:
    

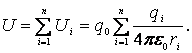     (1.15)

      Из формул (1.14) и (1.15) можно выделить отношение , которое называется потенциалом и является энергетической характеристикой электростатического поля:
    

      (1.16)

     Таким образом, потенциал в какой-либо точке электростатического поля есть физическая скалярная величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.
     Из формулы (1.16) с учетом (1.14) следует, что потенциал точки поля точечного заряда
    

     (1.17)

     где r – расстояние от заряда до заданной точки. Работа, совершаемая силами электростатического поля по перемещению заряда  из точки 1 в точку 2 (выражение (1.13)) может быть представлена как
    

        (1.18)  

      т.е. работа кулоновских сил численно равна произведению величины перемещаемого заряда на разность потенциалов в начальной и конечной точках поля. Из формулы (1.18) следует, что разность потенциалов двух точек электростатического поля – это физическая скалярная величина, определяемая работой, совершаемой кулоновскими силами при перемещении единичного положительного заряда из одной точки в другую.
     Если перемещать заряд  из произвольной точки за пределы поля, т.е. в бесконечность, где по условию потенциал равен нулю, то согласно (1.18) работа сил электростатического поля откуда
    

     (1.19)

      Таким образом, потенциал – это физическая величина, определяемая работой по перемещению единичного положительного заряда из данной точки поля в бесконечность.
     Единица потенциала – вольт (В): 1 В – это потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией в 1 Дж (см. формулу (1.16)):
    

     Из формул (1.15) и (1.16) вытекает, что если электростатическое поле создается несколькими зарядами, то потенциал точки поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:  
    

Проводники и диэлектрики в электрическом поле

Вещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в среднем по объемам, включающим большое число атомов или молекул, равно нулю. При наличии внешнего поля происходит перераспределение заряженных частиц, и в веществе возникает собственное электрическое поле. Полное электрическое поле складывается в соответствии с принципом суперпозиции из внешнего поля и внутреннего поля создаваемого заряженными частицами вещества.

Вещество многообразно по своим электрическим свойствам. Наиболее широкие классы вещества составляют проводники и диэлектрики.

Основная особенность проводников – наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника. Типичные проводники – металлы.

В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды (рис. 4.5.1). Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды – индукционными зарядами.

Индукционные заряды создают свое собственное поле которое компенсирует внешнее поле во всем объеме проводника: (внутри проводника).

Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника.

В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.

При внесении диэлектрика во внешнее электрическое поле в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.

Связанные заряды создают электрическое поле которое внутри диэлектрика направлено противоположно вектору напряженности внешнего поля. Этот процесс называется поляризацией диэлектрика. В результате полное электрическое поле внутри диэлектрика оказывается по модулю меньше внешнего поля

Физическая величина, равная отношению модуля напряженности внешнего электрического поля в вакууме к модулю напряженности полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.

Если двум изолированным друг от друга проводникам сообщить заряды q₁ и q₂, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников. Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U. Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q₁ = – q₂ = q. В этом случае можно ввести понятие электрической емкости.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

 

В системе СИ единица электроемкости называется фарад (Ф):

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рис. 4.6.1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния.

Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:

параллельно c=c1+c2+c3+….+cn

последовательно 1/c=1/c1+1/c2+1/c3+…+1/cn

энергия конденсатора w=cΔφ2/2

где Δφ-разность потенциалов.