Определение регулярного выражения

Определение 5.1.1. Регулярное множество над алфавитом $\Sigma$ определяется рекурсивно следующим образом: 0 является регулярным множеством; 1 является регулярным множеством; если $a \in \Sigma$ , то a является регулярным множеством; если e и f являются регулярными множествоми, то $(e \replus f)$ , $(e \redot f)$ и тоже являются регулярными множествоми. Других регулярных множеств нема.

Определение 5.1.1. Регулярное выражение над алфавитом $\Sigma$ определяется рекурсивно следующим образом: 0 является регулярным выражением; 1 является регулярным выражением; если $a \in \Sigma$ , то a является регулярным выражением; если e и f являются регулярными выражениями, то $(e \replus f)$ , $(e \redot f)$ и тоже являются регулярными выражениями.

Для экономии скобок будем считать, что операция ^* связывает сильнее (то есть имеет более высокий приоритет), чем умножение, а умножение связывает сильнее, чем сложение. Вместо $e \redot f$ часто пишут просто .

Пример 5.1.2. Пусть $\Sigma = \{ a , b \}$ . Тогда $( ( a \redot b )^* \redot ( 1 \replus a ) )$ является регулярным выражением над алфавитом $\Sigma$ .

Зам для каждого регулярного выражения можно построить регулярное множество обозначаемым этим выражением. Для каждого регулярного множества сожно найти покрайнемере одно регулярное выражение обозначающее это множество. Для каждого регулярного множества существует бесконечно много обозначающих его регулярных выражений

ОПР: два регулярных выражения равны, если они обозначают одно и то же множество.

Определение 5.1.3. Каждое регулярное выражение e над алфавитом $\Sigma$ задает (denotes, represents) некоторый язык над алфавитом $\Sigma$ (обозначение $\regval{e}$ ), определяемое рекурсивно следующим образом:

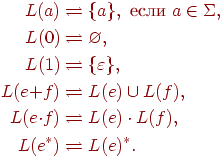
$\begin{align*} \regval{a} &\bydef \{ a \} ,\mathspace\text{если}\mathspace a \in \Sigma ,\\ \regval{0} &\bydef \varnothing ,\\ \regval{1} &\bydef \{ \varepsilon \} ,\\ \regval{e \replus f} &\bydef \regval{e} \cup \regval{f} ,\\ \regval{e \redot f} &\bydef \regval{e} \cdot \regval{f} ,\\ \regval{e^*} &\bydef \regval{e}^* . \end{align*}$

Заметим, что в правой части последнего выражения символом * обозначена итерация языка (см. определение 1.2.7).

Вместо $\regval{e}$ часто пишут просто e.

Пример 5.1.4. Пусть $\Sigma = \{ a , b \}$ . Согласно определению

$\regval{ ( ab )^* \redot ( 1 \replus a ) } \peq \{ (ab)^n \mid n \geq 0 \} \cup \{ (ab)^n a \mid n \geq 0 \} .$

Определение 5.1.5. Язык L называется регулярным если он задается некоторым регулярным выражением.

Определение 5.1.6. Пусть e - регулярное выражение. Тогда $e^+ \bydef e^* e$ .

5.2*. Свойства регулярных выражений

Лемма 5.2.1. Регулярные выражения образуют ассоциативное полукольцо с операциями $( 0 , \replus , 1 , \redot )$ , то есть для любых регулярных выражений e, f и g выполняются следующие тождества:

e+f = f+e;
e+0 = e;
;
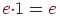$e \redot 1 = e$ ;
$1 \redot e = e$ ;
$(e \redot f) \redot g = e \redot (f \redot g)$ ;
$e \redot (f \replus g) = e \redot f \replus e \redot g$ ;
$(f \replus g) \redot e = f \redot e \replus g \redot e$ ;
$e \redot 0 = 0$ ;
$0 \redot e = 0$ .
e+e = e
e*=e+e*
0*=1
(e*)*=e*

Равенство понимается как равенство языков, задаваемых регулярными выражениями.