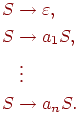3

3. Классы грамматик

Определение 1.5.1. Контекстной грамматикой (контекстно-зависимой грамматикой, грамматикой непосредственно составляющих, НС-грамматикой, грамматикой типа 1, context-sensitive grammar, phrase-structure grammar) называется порождающая грамматика, каждое правило которой имеет вид $\eta A \theta \to \eta \alpha \theta$ , где $A \in N$ , $\eta \in (N \cup \Sigma) ^*$ , $\theta \in (N \cup \Sigma) ^*$ , $\alpha \in (N \cup \Sigma) ^+$ .

Пример 1.5.2. Грамматика

$\begin{align*} S \; & {\to} \; T S , & A \; & {\to} \; a , \\ S \; & {\to} \; U S , & T A \; & {\to} \; A A T , \\ S \; & {\to} \; b , & U A b \; & {\to} \; b , \\ T b \; & {\to} \; A b , & U A A A \; & {\to} \; A A U \end{align*}$

не является контекстной (последние три правила не имеют требуемого вида).

Определение 1.5.3. Контекстно-свободной грамматикой (бесконтекстной грамматикой, КС-грамматикой, грамматикой типа 2, context-free grammar) называется порождающая грамматика, каждое правило которой имеет вид $A \to \alpha$ , где $A \in N$ , $\alpha \in (N \cup \Sigma) ^*$ .

Пример 1.5.4. Грамматика

$\begin{align*} S \; & {\to} \; ASTA , & AT \; & {\to} \; UT , \\ S \; & {\to} \; AbA , & UT \; & {\to} \; UV , \\ A \; & {\to} \; a , & UV \; & {\to} \; TV , \\ bT \; & {\to} \; bb , & TV \; & {\to} \; TA \end{align*}$

является контекстной, но не контекстно-свободной (последние пять правил не имеют требуемого вида).

Определение 1.5.5. Линейной грамматикой (linear grammar) называется порождающая грамматика, каждое правило которой имеет вид $A \to u$ или $A \to u B v$ , где $A \in N$ , $u \in \Sigma ^*$ , $v \in \Sigma ^*$ , $B \in N$ .

Грамматика

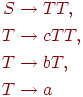
$\begin{align*} S \; & {\to} \; TT , \\ T \; & {\to} \; cTT , \\ T \; & {\to} \; bT , \\ T \; & {\to} \; a \end{align*}$

является контекстно-свободной, но не линейной (первые два правила не имеют требуемого вида).

Определение 1.5.7. Праволинейной грамматикой (рациональной грамматикой, грамматикой типа 3, right-linear grammar) называется порождающая грамматика, каждое правило которой имеет вид $A \to u$ или $A \to u B$ , где $A \in N$ , $u \in \Sigma ^*$ , $B \in N$ .

Пример 1.5.8. Грамматика

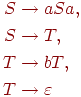
$\begin{align*} S \; & {\to} \; aSa , \\ S \; & {\to} \; T , \\ T \; & {\to} \; bT , \\ T \; & {\to} \; \varepsilon \end{align*}$

является линейной, но не праволинейной (первое правило не имеет требуемого вида).

Пример 1.5.9. Грамматика

$\begin{align*} S \; & {\to} \; T , \\ U \; & {\to} \; abba \end{align*}$

праволинейная. Она порождает язык $\varnothing$ .

Пример 1.5.10. Грамматика

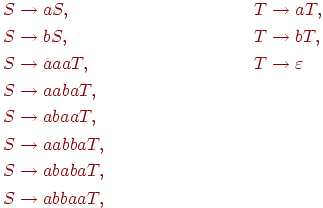
$\begin{align*} S \; & {\to} \; aS , & T \; & {\to} \; aT , \\ S \; & {\to} \; bS , & T \; & {\to} \; bT , \\ S \; & {\to} \; aaaT , & T \; & {\to} \; \varepsilon \\ S \; & {\to} \; aabaT , \\ S \; & {\to} \; abaaT , \\ S \; & {\to} \; aabbaT , \\ S \; & {\to} \; ababaT , \\ S \; & {\to} \; abbaaT , \end{align*}$

праволинейная.

Пример 1.5.11. Грамматика

$\begin{align*} S \; & {\to} \; \varepsilon , & T \; & {\to} \; abaT , \\ S \; & {\to} \; aaaS , & T \; & {\to} \; baaT , \\ S \; & {\to} \; abbS , & T \; & {\to} \; bbbT , \\ S \; & {\to} \; babS , & T \; & {\to} \; bbaS \\ S \; & {\to} \; aabT , \end{align*}$

праволинейная. Обобщенный вариант языка, порождаемого этой грамматикой, используется в доказательстве разрешимости арифметики Пресбургера.

Определение 1.5.12. Правила вида $\alpha \to \varepsilon$ называются $\varepsilon$ -правилами или эпсилон-правилами.

Лемма 1.5.13. Каждая праволинейная грамматика является линейной. Каждая линейная грамматика является контекстно-свободной. Каждая контекстно-свободная грамматика без $\varepsilon$ -правил является контекстной грамматикой.

Определение 1.5.14. Классы грамматик типа 0, 1, 2 и 3 образуют иерархию Хомского (Chomsky hierarchy).

Определение 1.5.15. Язык называется языком типа 0 (контекстным языком, контекстно-свободным языком, линейным языком, праволинейным языком), если он порождается некоторой грамматикой типа 0 (соответственно контекстной грамматикой, контекстно-свободной грамматикой, линейной грамматикой, праволинейной грамматикой). Контекстно-свободные языки называются также алгебраическими языками.

Пример 1.5.16. Пусть дан произвольный алфавит

$\Sigma = \{ a_1 , \ldots , a_n \} .$

Тогда язык $\Sigma ^*$ является праволинейным, так как он порождается грамматикой

$\begin{align*} S \; & {\to} \; \varepsilon , \\ S \; & {\to} \; a_1 S , \\ & \vdots\\ S \; & {\to} \; a_n S . \end{align*}$