1

1.4. Порождающие грамматики

Определение 1.4.1. Порождающей грамматикой (грамматикой типа 0, generative grammar, rewrite grammar) называется четверка $G \rightleftharpoons \langle N , \Sigma , P , S \rangle$ , где N и $\Sigma$ - конечные алфавиты, $N \cap \Sigma = \varnothing$ , $P \subset (N \cup \Sigma) ^+ \times (N \cup \Sigma) ^*$ , P конечно и $S \in N$ . Здесь $\Sigma$ - основной алфавит (терминальный алфавит), его элементы называются терминальными символами или терминалами (terminal), N - вспомогательный алфавит (нетерминальный алфавит), его элементы называются нетерминальными символами, нетерминалами, вспомогательными символами или переменными (nonterminal, variable), S - начальный символ (аксиома, start symbol). Пары $( \alpha , \beta ) \in P$ называются правилами подстановки, просто правилами или продукциями (rewriting rule, production) и записываются в виде $\alpha \rightarrow \beta$ .

Пример 1.4.2. Пусть даны множества N = {S}, $\Sigma = \{ a , b , c \}$ , $P = \{ S \rightarrow acSbcS ,\ cS \rightarrow \varepsilon \}$ . Тогда $\langle N , \Sigma , P , S \rangle$ является порождающей грамматикой.

Замечание 1.4.3. Будем обозначать элементы множества $\Sigma$ строчными буквами из начала латинского алфавита, а элементы множества N - заглавными латинскими буквами. Обычно в примерах мы будем задавать грамматику в виде списка правил, подразумевая, что алфавит N составляют все заглавные буквы, встречающиеся в правилах, а алфавит $\Sigma$ - все строчные буквы, встречающиеся в правилах. При этом правила порождающей грамматики записывают в таком порядке, что левая часть первого правила есть начальный символ S.

Замечание 1.4.4. Для обозначения n правил с одинаковыми левыми частями $\alpha \rightarrow \beta_1,\ldots, \alpha \rightarrow \beta_n$ часто используют сокращенную запись $\alpha \rightarrow \beta_1 \mid \ldots \mid \beta_n$ .

Определение 1.4.5. Пусть дана грамматика G. Пишем $\phi \underset { G } {\Rightarrow } \psi$ , если $\phi = \eta \alpha \theta$ , $\psi = \eta \beta \theta$ и $( \alpha \rightarrow \beta ) \in P$ для некоторых слов $\alpha, \; \beta, \; \eta, \; \theta$ в алфавите $N \cup \Sigma$ . Если $\phi \underset{ G }{\Rightarrow } \psi$ , то говорят, что слово $\psi$ непосредственно выводимо из слова $\phi$ .

Определение 1.4.8. Если $\omega_0 \underset{ G }{\Rightarrow } \omega_1 \underset{ G }{\Rightarrow } \ldots \underset{ G }{\Rightarrow } \omega_n$ , где $n \geqslant 0$ , то пишем ${\omega_0 \overset * {\underset{ G }{\Rightarrow}} \omega_n}$ и говорим, что слово $\omega_n$ выводимо из слова $\omega_0$ . Другими словами, бинарное отношение ${\overset * {\underset{ G }{\Rightarrow}}}$ является рефлексивным, транзитивным замыканием бинарного отношения ${\underset{ G }{\Rightarrow}}$ , определенного на множестве $(N \cup \Sigma) ^*$ .

При этом последовательность слов $\omega_0, \omega_1,\ldots, \omega_n$ называется выводом (derivation) слова $\omega_n$ из слова $\omega_0$ в грамматике G. Число n называется длиной (количеством шагов) этого вывода.

Замечание 1.4.9. В частности, для всякого слова $\omega \in (N \cup \Sigma) ^*$ имеет место $\omega \oversуt * {\underset{ G }{\Rightarrow}} \omega$ (так как возможен вывод длины 0).

Пример 1.4.10. Пусть $G = \langle \{ S \} , \{ a , b \} , \{ S \rightarrow aSa ,\ S \rightarrow b \} , S \rangle$ . Тогда $aSa \overset * {\underset{ G }{\Rightarrow }} aaaaSaaaa$ . Длина этого вывода - 3.

Определение 1.4.11. Язык, порождаемый грамматикой G, - это множество $L(G) \rightleftharpoons \{ \omega \in \Sigma ^* \mid S \overset * {\underset{ G }{\Rightarrow}} \omega \}$ . Будем также говорить, что грамматика G порождает (generates) язык L(G).

Определение 1.4.14. Две грамматики эквивалентны, если они порождают один и тот же язык.

Пример 1.4.15. Грамматика

$\begin{align*} S \; & {\to} \; abS , \\ S \; & {\to} \; a \end{align*}$

и грамматика

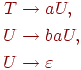
$\begin{align*} T \; & {\to} \; aU , \\ U \; & {\to} \; baU , \\ U \; & {\to} \; \varepsilon \end{align*}$

эквивалентны.

Практическое применение грамматик связанно с решением проблемы распознавания. Проблема распознавания разрешима, если существует такой алгоритм, который за конечное число шагов дает ответ на вопрос: принадлежит ли произвольная цепочка над основным словарем грамматики языку, порождаемому этой грамматикой, если такой алгоритм существует, то он называется распознаваемым. Если число шагов алгоритма распознавания зависит от длинны цепочки и может быть оценено до выполнения алгоритма, язык называется легко распознаваемым.