1

1.Формальные языки

Определение 1.1.1. Будем называть натуральными числами неотрицательные целые числа. Множество всех натуральных чисел {0, 1, 2, ...} обозначается N.

Определение 1.1.2. Алфавитом называется конечное непустое множество. Его элементы называются символами (буквами).

Определение 1.1.3.Словом (цепочкой, строкой, string) в алфавите $\Sigma$ называется конечная последовательность элементов $\Sigma$ .

Пример 1.1.4. Рассмотрим алфавит $\Sigma$ = {a, b, c}. Тогда baaa является словом в алфавите $\Sigma$ .

Определение 1.1.5. Слово, не содержащее ни одного символа (то есть последовательность длины 0), называется пустым словом и обозначается $\varepsilon$ .

Определение 1.1.6. Множество всех слов в алфавите $\Sigma$ обозначается $\Sigma ^*$ .

Замечание 1.1.7. Множество $\Sigma ^*$ счетно. В самом деле, в алфавите $\Sigma$ множество всех слов данной длины конечно, следовательно, $\Sigma ^*$ является объединением счетного числа конечных множеств.

Определение 1.1.8. Множество всех непустых слов в алфавите $\Sigma$ обозначается $\Sigma ^+$ .

Пример 1.1.9. Если $\Sigma$ = {a}, то $\Sigma ^+$ = {a,aa,aaa,aaaa,...}.

Определение 1.1.10. Если $L \subseteq \Sigma ^*$ , то L называется языком (или формальным языком) над алфавитом $\Sigma$ .

Поскольку каждый язык является множеством, можно рассматривать операции объединения, пересечения и разности языков, заданных над одним и тем же алфавитом (обозначения $L_1 \cup L_2,\; L_1 \cap L_2,\; L_1 - L_2$ ).

Пример 1.1.11. Множество {a, abb} является языком над алфавитом {a, b}.

Определение 1.1.12. Пусть $L \subseteq \Sigma ^*$ . Тогда язык $\Sigma ^* - L$ называется дополнением языка L относительно алфавита $\Sigma$ . Когда из контекста ясно, о каком алфавите идет речь, говорят просто, что язык $\Sigma ^* - L$ является дополнением языка L.

Определение 1.1.13. Если x и y - слова в алфавите $\Sigma$ , то слово xy (результат приписывания слова y в конец слова x) называется конкатенацией, (катенацией, сцеплением) слов x и y. Иногда конкатенацию слов x и y обозначают $x \cdot y$ .

Определение 1.1.14. Если x - слово и $n \in N$ , то через xⁿ обозначается слово $\underbrace{ x \cdot x \cdot \ldots \cdot x }_{n \text{ раз}}$ . Положим $x^0 \rightleftharpoons \varepsilon$ (знак $\rightleftharpoons$ читается "равно по определению"). Всюду далее показатели над словами и символами, как правило, являются натуральными числами.

Пример 1.1.15. По принятым соглашениям ba³ = baaa и (ba)³ = bababa.

Пример 1.1.16. Множество $\{ a^k b a^l \mid k \leqslant l \}$ является языком над алфавитом {a,b}. Этот язык содержит слова b, ba, aba, baa, abaa, baaa, aabaa, abaaa, baaaa и т. д.

Определение 1.1.17. Длина слова w, обозначаемая |w|, есть число символов в w, причем каждый символ считается столько раз, сколько раз он встречается в w.

Пример 1.1.18. Очевидно, что |baaa| = 4 и $| \varepsilon | = 0$ .

Определение 1.1.19. Через |w|_a обозначается количество вхождений символа a в слово w.

Пример 1.1.20. Если $\Sigma = \{ a , b , c \}$ , то |baaa|_a = 3, |baaa|_b = 1 и |baaa|_c = 0.

1.2. Операции над языками

Определение 1.2.1. Пусть $L_1 , L_2 \subseteq \Sigma ^*$ . Тогда

$L_1 \cdot L_2 \rightleftharpoons \{ x y \mid x \in L_1, \; y \in L_2 \} .$

Язык $L_1 \cdot L_2$ называется конкатенацией языков L₁ и L₂.

Пример 1.2.2. Если L₁ = {a,abb} и L₂ = {bbc,c}, то $L_1 \cdot L_2 = \{ ac , abbc , abbbbc \}$ .

Определение 1.2.4. Пусть $L \subseteq \Sigma ^*$ . Тогда

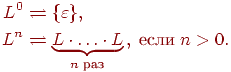
$\begin{align*} L^0 &\rightleftharpoons \{ \varepsilon \} ,\\ L^n &\rightleftharpoons \underbrace{ L \cdot \ldots \cdot L }_{n \; \text{раз}} \,, \; \text{если} \; n > 0 . \end{align*}$

Пример 1.2.5. Если L = {a^kba^l | 0 < k < l}, то L² = {a^kba^lba^m | 0 < k < l - 1, m > 1}.

Определение 1.2.7. Итерацией языка (Kleene closure) языка L (обозначение L^*) называется язык

$\bigcup \limits_{ n \in \mathbb{N} } L^n.$

Эта операция называется также звездочкой Клини (Kleene star, star operation).

Пример 1.2.8. Если $\Sigma = \{ a , b \}$ и L = {aa,ab,ba,bb}, то

$L^* = \{ w \in \Sigma ^* \mid | w | \; \vdots \; 2 \} .$

Определение 1.2.11. Обращением или зеркальным образом слова w (обозначается w^R) называется слово, в котором символы, составляющие слово w, идут в обратном порядке.

Пример 1.2.12. Если w = baaca, то w^R = acaab.

Определение 1.2.13. Пусть $L \subseteq \Sigma ^*$ . Тогда

$L \reverse \rightleftharpoons \{ w \reverse \mid w \in L \} .$

Определение 1.2.15. Говорят, что слово x - префикс (начало) слова y (обозначение $x \sqsubset y$ ), если y = xu для некоторого слова u.

Пример 1.2.16. Очевидно, что $\varepsilon \sqsubset baa$ , $b \sqsubset baa$ , $ba \sqsubset baa$ и $baa \sqsubset baa$ .

Определение 1.2.17. Пусть $L \subseteq \Sigma ^*$ . Тогда через Pref(L) обозначается множество, состоящее из всех префиксов слов языка L:

$\mathrm{Pref} ( L ) \rightleftharpoons \{ x \mid ( \exists y \in L )\, x \sqsubset y \} .$

Определение 1.2.18 Говорят, что слово x - суффикс (конец) слова y (обозначение $x \sqsupset y$ ), если y = ux для некоторого слова u.

Определение 1.2.19. Пусть $L \subseteq \Sigma ^*$ . Тогда через Suf(L) обозначается множество, состоящее из всех суффиксов слов языка L:

$\mathrm{Suf} ( L ) \rightleftharpoons \{ x \mid ( \exists y \in L )\, x \sqsupset y \} .$

Определение 1.2.20. Говорят, что слово x - подслово (substring) слова y, если y = uxv для некоторых слов u и v.