Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Электрический заряд обычно обозначается буквами q или Q.

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

• Существует два рода электрических зарядов, условно названных положительными и отрицательными.
• Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
• Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

q₁ + q₂ + q₃ + ... +q_n = const 

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.

Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

 

Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 4.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.

Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).

Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.

Коэффициент k в системе СИ обычно записывают в виде:

 

где – электрическая постоянная. 

Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Для количественного определения электрического поля вводится силовая характеристика напряженность электрического поля.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:

 

Напряженность электрического поля – векторная физическая величина. Направление вектора совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.

Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

 

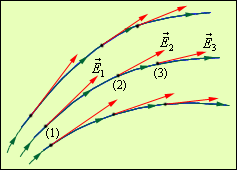
Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора в каждой точке совпадало с направлением касательной к силовой линии (рис. 4.2.1). При изображении электрического поля с помощью силовых линий, их густота должна быть пропорциональна модулю вектора напряженности поля.

HРабота поля по замкнутому полю равна 0

Ai=q*e*di*cosα

A=0, то поле потенциальное.

Теорема Гаусса

Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.

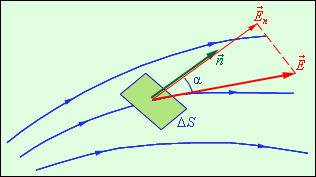
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Понятие потока вектора аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора на площадь ΔS и на косинус угла α между вектором и нормалью к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 4.3.1):

где – модуль нормальной составляющей поля  

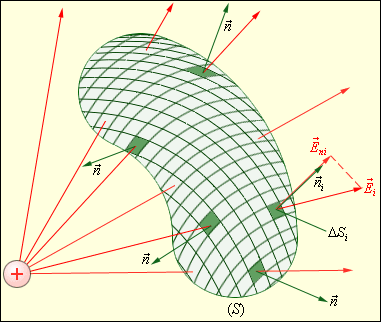
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔS_i, определить элементарные потоки поля через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора через замкнутую поверхность S (рис. 4.3.2):

 

В случае замкнутой поверхности всегда выбирается внешняя нормаль.

Теорема Гаусса утверждает:

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀.

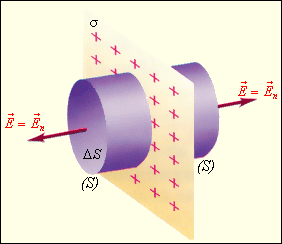
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 4.3.5).

В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает:

где σ – поверхностная плотность заряда, то есть заряд, приходящийся на единицу площади. 

Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.